ПРЯМАЯ И ОБРАТНАЯ
ПРОПОРЦИОНАЛЬНОСТЬ.
I.
Прямая пропорциональность.
О: Функция вида y = kx + b называется линейной функцией.
k, b - числа (параметры), x - переменная (аргумент)
О: Линейная
функция вида y = kx называется прямой пропорциональностью.
Свойства
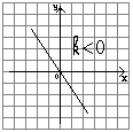
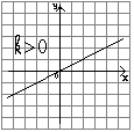
функции y = kx График функции y = kx
1.
Dy = R
2.
Корни: x = 0
3.
При k > 0 Þ y > 0 при x Î (0;+¥)
y < 0 при x Î (-¥; 0)
При k < 0 Þ y > 0 при x Î (-¥; 0)
y < 0 при x Î (0;+¥)
4.
При k > 0 Þ функция возрастает
При k < 0 Þ функция убывает
5.
Экстремумов нет.
6.
Зная две точки (x1
,y1) и (x2
,y2) можно найти: 1.
Угол наклона прямой к оси ОХ: tga = k = (y2 -
y1)/(x2 - x1)
2. Уравнение прямой: y = y1 + k(x2 - x1)
Наибольшего и наименьшего значения нет.
7.
Ey = R
8.
Нечётная, непериодическая.
График -
прямая, строим по двум точкам.
Замечание: График функции
y = kx + b получаем перемещением графика
функции y = kx по вертикали:
если b > 0 , то вверх на b
если b < 0 , то вниз на b
II. Обратная пропорциональность.
О: Функция
вида y = k / x называется обратной
пропорциональностью.
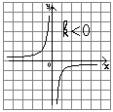
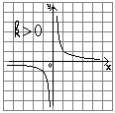
Свойства функции y = k / x График функции
y = k / x
1.
Dy = (-¥; 0)È (0; +¥)
2.
Корней нет
3.
При k > 0 Þ y > 0 при x Î (0;+¥)
y < 0 при x Î (-¥; 0)
При k < 0 Þ y > 0 при x Î (-¥; 0)
y < 0 при x Î (0;+¥)
4.
При k > 0 Þ функция убывает
При k < 0 Þ функция возрастает
5.
Экстремумов нет.
6.
Зная координаты точки (x1
,y1), можно
найти k: k = x1 · y1
Наибольшего и наименьшего значения нет.
7.
Ey = (-¥; 0)È (0; +¥)
8.
Нечётная, непериодическая.
График -
гипербола, строим заполняя таблицу.
Примеры таких зависимостей: