КВАДРАТИЧНАЯ  ФУНКЦИЯ.

 

О: Функция вида  y = ax ² + bx + c  называется квадратичной функцией, где  a, b, c - числа.

     a¹ 0 - первый коэффициент, b - второй ..., c - свободный член,  x - переменная (аргумент)

О: Выражение вида  ax ² + bx + c  называется квадратным трёхчленом.

О: График квадратичной функции называется параболой.

План построения параболы:

 

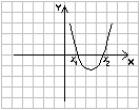
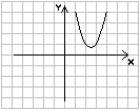
1. Ветви при a > 0 - вверх

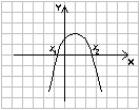
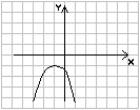
              при a < 0 - вниз

2.   Вершина О(m, n) , где:

            m = -b / 2a

            n = -D / 4a

3.  Таблица               -2             -1                      +1          +2

x			[ m]
y

4.   Строим параболу:

 

 

Решение квадратного уравнения:

            ax ² + bx + c = 0

1 способ:

Вычислить дискриминант: D = b ² - 4ac

                                        - b ± Ö D

Вычислить корни:  x_1,2 = ¾¾¾¾

                                            2a

2 способ:

По теореме Виета:

                          ì x₁ + x₂ = -b / a

 í

î x₁ ·  x₂ =  c / a

при  а = 1 Þ   

                          ì x₁ + x₂ = -b

 í

î x₁ ·  x₂ =  c

 

            a > 0                            a > 0                            a < 0                            a < 0

            D > 0                           D < 0                           D > 0                           D < 0

      

 

Свойства функции  y = ax ² + bx + c

1.   Область определения (-¥;+¥)

2.   Корни:        при D > 0  - 2 корня

                        при D = 0 - 1 корень

                        при D < 0 - нет корней

3.   Промежутки знакопостоянства:

            (см . графики)

4.   Промежутки монотонности:

            (см . графики)

5.   Экстремумы:

            при  а > 0 - точка минимума (m;n)

            при a < 0 - точка максимума (m;n)

6.   Наибольшее и наименьшее значение:

            при  a > 0 - наибольшего значения нет

                               наименьшее = n

            при  a < 0 - наибольшее = n

                              наименьшего значения нет

7.   Область значений:

            при  a > 0  E_y = [n;+¥)

            при  a < 0 E_y = (-¥; n]

8.   Ни чётная, ни нечётная

    Непериодическая

 

3 способ:  если  b - чётное:

Вычислить дискриминант: D₁ = (b/2) ² - ac

 

                                        - b/2 ± Ö D₁

Вычислить корни:  x_1,2 = ¾¾¾¾

                                             a

 

Разложение квадратного трёхчлена на множители:

ax ² + bx + c = a(x - x₁ )(x - x₂ )

 

Решение квадратных неравенств:

     ax ² + bx + c > 0   или    ax ² + bx + c < 0

если  D > 0:

            a > 0                            a < 0   

     

если  D = 0:

            a > 0                            a < 0   

     

если  D < 0:

            a > 0                            a < 0

         

и выписывай ответ...